Practice sketching each curve freehand and label important values on each axis. As the curve repeats every 180^o, the next asymptote is at 270^o and so on.Įach trigonometric graph is a curve and therefore the only time you are required to use a ruler is to draw a set of axes. The tangent function has an asymptote at 90^o because this value is undefined.
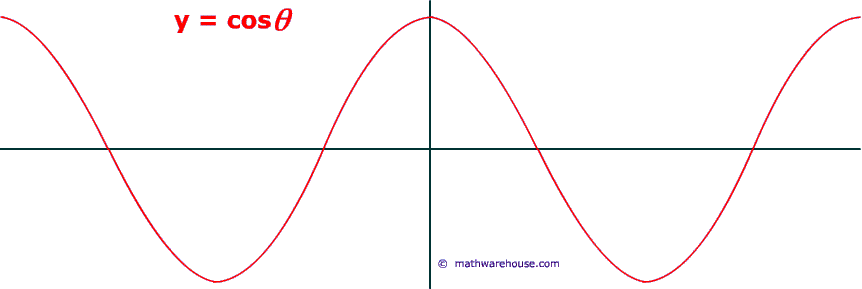
Asymptotes are drawn incorrectly for the graph of the tangent function. A tip to remember is that you “sine up” from 0 for the sine graph so the line is increasing whereas you “cosine down” from 1 so the line is decreasing for the cosine graph. The sine and cosine graphs are very similar and can easily be confused with one another. When you are finding the value of \theta using a trigonometric graph, only one value is calculated when there are more points of intersection.įor example, only the value of 65^o is read off the graph. Drawing the horizontal line only to one intersection point. Now that we have generated the graph of \cos(\theta), we need to be able to interpret it to find values of \theta and \cos(\theta) for any value between the range -360^o \leq \theta \leq 360^o (values for \theta between -360^o and 360^o. Top tip: you can remember the coordinate order as alphabetical x before y and cos before sin to get the coordinate (\cos(\theta), \ \sin(\theta)) Here are a couple of examples to help you. You should be able to interpret the unit circle to determine the value of \theta. For more information, see the lesson on transformations of trigonometric graphs. The cosine wave can have different amplitudes when we transform the function. The maximum value is therefore 1, and the minimum value is -1. The function of \cos(\theta) can be described as a wave, namely the cosine wave, with an amplitude of 1 because the function is limited between the values of -1 and 1. The graph is continuous for both positive and negative values of \theta and has a period of 360^o (this means that the graph repeats every 360^o ). The graph does not pass through the origin unlike the graphs for \sin(\theta) and \tan(\theta). We can also turn anticlockwise which would give us the negative value for the value of \cos(\theta). \cos(\theta) is as periodic function as we could continue to turn around the origin from the positive x axis beyond 360^o. COSINE GRAPH FULL
Continuing the point around the unit circle back to the coordinate (1,0), we get \cos(360)=1 as \theta has made a full turn back to the positive x axis. At the point (0,-1) we can say \cos(270)=0 as the angle \theta is 270^o. At the point (-1,0) we can say that \cos(180)=-1 as the angle \theta from the positive x axis is now 180^o. At the point (0,1) we can say that \cos(90)=0 as the angle \theta is equal to 90^o. 
At the point (1,0) we can say that \cos(0)=1 as the angle \theta would be 0^o. 
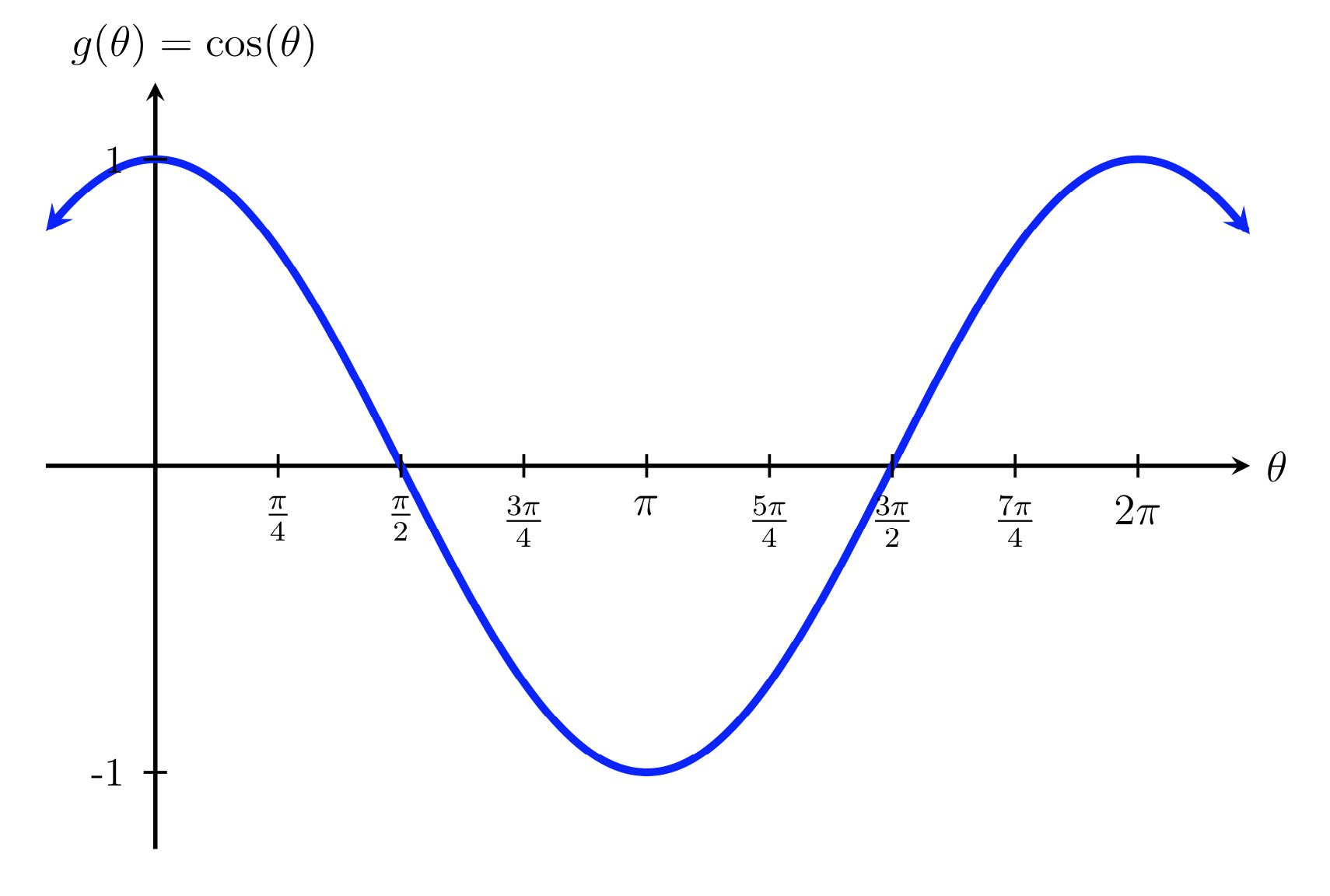
The x value of the coordinate on the unit circle gives us the value for \cos(\theta) so: The point on the unit circle is therefore the coordinate ( \cos(\theta), \ \sin(\theta) ): This means that the width of the triangle is equal to \cos(\theta) and the height of the triangle is equal to \sin(\theta). Here we can see that for \cos(\theta)=\frac For each triangle, the hypotenuse is the same but the length of the adjacent side and the associated angle change. Let’s look at 3 triangles where we would use the cosine ratio to calculate the size of the angle \theta.
When the angle is in the first and second quadrants, sine is positive, and when the angle is in the 3rd and 4th quadrants, sine is negative.Remember that \cos(\theta) is a relationship between the adjacent side and the hypotenuse of a right angle triangle:. Radians are much more useful in engineering and science compared to degrees. All the graphs in this chapter deal with angles in radians. The rotation angle in radians is the same as the time (in seconds). This indicates how much energy is involved in the quantity being graphed. This quantity of a sine curve is called the amplitude of the graph. In the interactive, when the radius of the circle was `50` units then the curve went up to `50` units and down to `-50` units on the y-axis. The period is the time it takes to go through one complete cycle. The shape of the sine curve forms a regular pattern (the curve repeats after the wheel has gone around once). The relationship between the cosines unit circle on the left and its more horizontal graph on the right is a little harder to see here, because the unit circles output line (the purple line zipping from side to side) is horizontal while the standard graphs output line (also purple, going above and below the x-axis) is vertical.But you can see how those two purple lines have the same length. Copyright © Frame rate: 0 Did you notice?
0 kommentar(er)
